CNN Building Blocks - Basic

作者 Mingjiang Shi 日期 2019-06-09
deeplearning
CNN Building Blocks - Basic

卷积操作

CNN中的C是Convolutional，也就是卷积。我们首先来看看卷积是什么含义。假设有一根针掉在铺面马赛克的地板上，由于针太小，马赛克的颜色也比较暗，我们无法一眼找到针在哪里。于是我们拿着一个特制的方形有色镜片（该镜片可以过滤到不相干的颜色，有助于看清楚针）在地上从左到右，从上到下，一格一格地找。最终，我们是一定可以找到针的。CNN的卷积操作和这个例子非常类似。我们首先定义下相关的概念。

  • kernel：有的文献中也叫filter，kernel是一个k x k的矩阵，它就类似上面例子中的有色镜片，可以从图片中提取出相应的特征。
  • stride: 类似上面的例子，stride表示kernel在图片上移动时，每次移动几个格子。

有了上面两个概念，我们来看个例子，假设我们有下面这个3x3的kernel:

[
  [0, 1, 2],
  [2, 2, 0],
  [0, 1, 2]
]

利用这个kernel对下图进行卷积操作的过程如下图所示：

图片来自：https://arxiv.org/pdf/1603.07285.pdf

首先，将kernel与左上角对齐，由于kernel的尺寸为3x3，所以它覆盖了图片左上角的3x3个像素，将对应位置的数值相乘后相加即可得到右边图片左上角格子上的值。然后依次从左往右，从上往下移动kernel对剩下的像素进行卷积操作，即可得到最右下角的最终结果。

从上图中，我们可以看到原图的9个像素经过卷积操作后变成了目标图的1个像素，这是一个多对一的操作。卷积操作是从原图中提取特征，经过卷积操作后得到的3x3矩阵叫做feature map（特征图）。

stride有什么用？

上图中stride为1，即kernel每次移动一个像素。如果stride为2的话，kernel每次移动2个像素，这样最终得到的feature map就只有2x2了。

如果输入图不止一个通道呢？

上图中，图片只有1个通道，可以认为是黑白图。对于彩色图片，有RGB三个通道，卷积操作有什么变化呢？

  1. 输入图片有c个通道，那么kernel也需要有c个通道，也就是说kernel变成了三维，其shape变成了(k, k, c)，可以理解为c个k x k大小的kernel的重叠在一起（注意：它们还是一个kernel）。卷积运算就是将c个k x k的kernel分别与输入图的c个通道的对应位置的数值相乘后再相加。参见下图。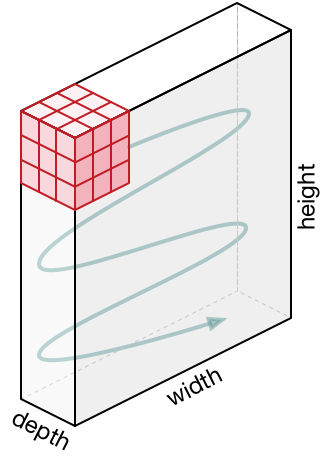

    图片来自：https://machinethink.net

  2. 最终得到特征图的维度还是二维的。

如果有多个kernel呢？

从上面可以看到一个kernel只提取一种特征，因为kernel的参数是确定的。如果我们需要提取多种特征，就需要多个kernel。那么最终得到的feature map也就变成了3维了，可以看成是每个kernel提取特征得到的feature map的叠加。如下图所示：

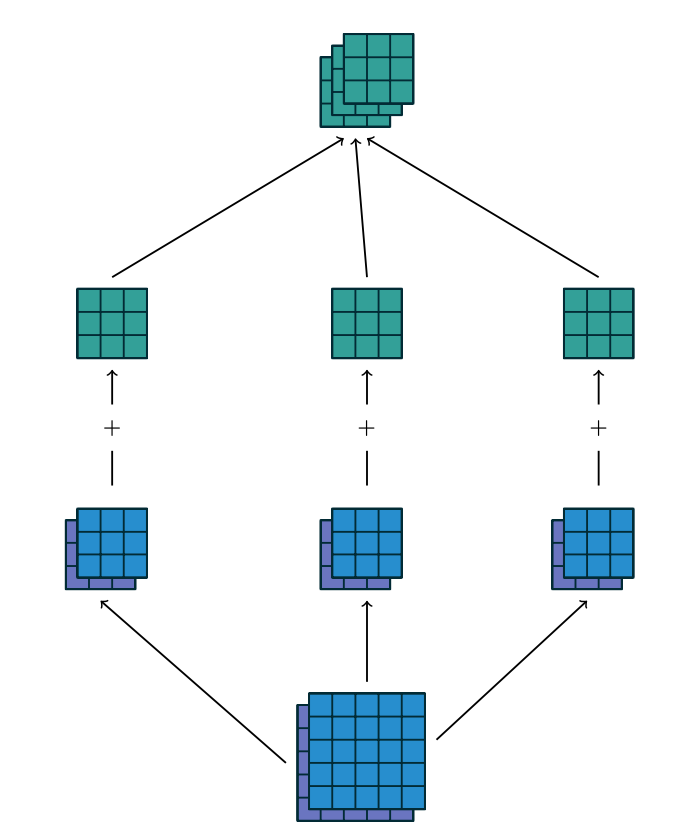
图片来自：https://arxiv.org/pdf/1603.07285.pdf

最下方为输入图，该输入图为有2个通道，经过三个kernel（注意：每个kernel也是有2个通道的）处理后，每个kernel得到一个3x3的feature map，将他们叠加在一起后得到一个长宽均为3，有3个通道的feature map。

padding是什么？

padding就是在输入图的四周补0，从而增加输入图的长宽，padding = 1则补一圈0，长宽各增加1。合理选择padding, kernel和stride的大小，可以使得输出图的长宽与输入图的长宽保持一致。

卷积操作的参数量和计算量

我们来看看卷积操作需要的参数数量和计算量。我们都用w * h * c的格式来表示图像的长宽和通道数，为了简化，我们将认为图像的长宽相同。假设输入的图像为Di x Di * M, 输出的图像为Dj * Dj * N，kernel的shape为K * K * M，总共需要N个这样的Kernel。记住一点：Kernel的通道数与输入图像的通道数一致，Kernel的个数与输出通道数一致。

这里需要注意的是，Kernel的长宽（也就是上面的K）和输出的特征图的通道数M是设计网络的时候需要确定的，也就是说要我们需要事先决定Kernel的长宽和个数。而输出图的长宽(Dj)是根据输入图的长宽，Kernel的长宽，stride和padding等因素计算出来的（具体计算公式可以参考相关论文）。kernel中每个元素的值是需要用数据训练出来的。

由此可见，一个卷积操作的参数量为K * K * M * N，kernel中的每个值都是需要训练的参数。如果考虑偏置量的话，则再加上N（每个输出通道上增加1个参数），在比较参数量的时候通常忽略偏置量。

卷积操作的计算量怎么计算呢？我们从输出图像的角度来考虑，输出图像总共有Dj * Dj * N个值需要计算，每个值都是由kernel在输入图像上经过卷积操作得来，根据卷积操作的逻辑，每个卷积需要K * K * M次乘法和加法完成。因此，对输入图进行一次完整的卷积计算需要的计算量即为Dj * Dj * N * K * K * M，它只与输出图像和Kernel有关，与输入的长宽无关。

卷积小结

在计算机视觉领域，卷积通常处理的是3维向量（暂不考虑batch），分别对应到图像的长宽和通道数。kernel就类似于滤镜，不同的kernel可以从输入图中过滤中不同的东西。kernel的长宽是网络设计时需要决定的参数，其通道数与输入图像的通道数一致。kernel的数量也是网络设计时需要决定的参数。它的数量与输出图像的通道数一致。

直观上来讲，卷积操作就是设计不同的kernel来从输入图中提取不同的特征，每个kernel只负责一种特征。仍不住再举个简单的例子，假设输入图是w h 1的，每个像素是int32值，从低到高，每8位分别表示RGB的值。此时，我们就可以设计3个1x1x1的kernel，每个kernel过滤一种颜色，3个kernel就可以将输入图转为w h 3的RGB方式表示的图像。原始输入图只有1个通道，经过三个kernel处理后就变成了RGB三个通道。

以上就是CNN网络中最基础的卷积操作。

Pooling

Pooling比卷积要简单，可以用与理解卷积相同的方式来理解Pooling。Pooling就相当于把Kernel区域的输入图的值取最大值或者取平均值。如果取最大值就是MaxPooling，如果取平均值就是AveragePooling。下图为MaxPooling的示意图。可见，经过Pooling以后，输入图的长宽变小。

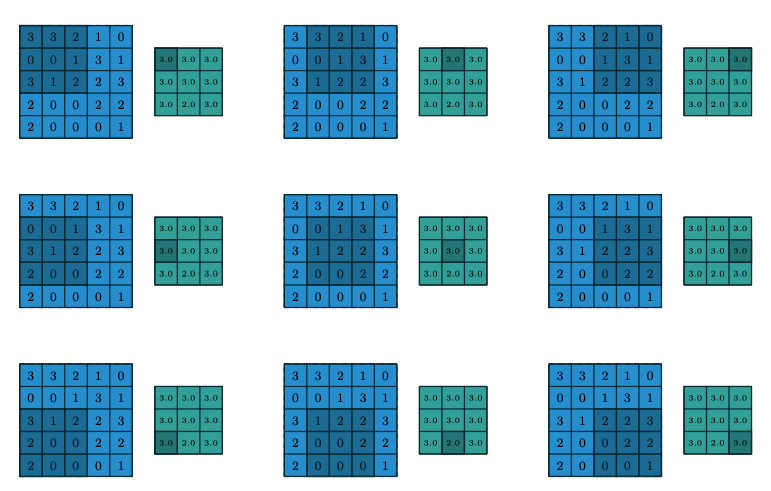
图片来自：https://arxiv.org/pdf/1603.07285.pdf

示例

下面我们用Keras来构建一个简单的CNN网络：

from keras import Model, Sequential
from keras.layers import Conv2D, AveragePooling2D

model = Sequential()
model.add(Conv2D(32, (3,3), name='conv1', padding='same', input_shape=(128,128,3), activation='relu'))
model.add(AveragePooling2D((2,2), name='ap1'))

model.add(Conv2D(64, (3,3), name='conv2', padding='same', activation='relu'))
model.add(AveragePooling2D((2,2), name='ap2'))

model.add(Conv2D(128, (3,3), name='conv3', padding='same', activation='relu'))
model.add(AveragePooling2D((2,2), name='ap3'))

model.add(Conv2D(256, (3,3), name='conv4', padding='same', activation='relu'))
model.add(AveragePooling2D((2,2), name='ap4'))

print(model.summary())

Output:
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv1 (Conv2D)               (None, 128, 128, 32)      896       
_________________________________________________________________
ap1 (AveragePooling2D)       (None, 64, 64, 32)        0         
_________________________________________________________________
conv2 (Conv2D)               (None, 64, 64, 64)        18496     
_________________________________________________________________
ap2 (AveragePooling2D)       (None, 32, 32, 64)        0         
_________________________________________________________________
conv3 (Conv2D)               (None, 32, 32, 128)       73856     
_________________________________________________________________
ap3 (AveragePooling2D)       (None, 16, 16, 128)       0         
_________________________________________________________________
conv4 (Conv2D)               (None, 16, 16, 256)       295168    
_________________________________________________________________
ap4 (AveragePooling2D)       (None, 8, 8, 256)         0         
=================================================================
Total params: 388,416
Trainable params: 388,416
Non-trainable params: 0
_________________________________________________________________
None

输入图的shape为(128,128,3)，也就是长宽均为128，有3个通道的图片。经过4层卷积和Pooling后变成了（8 x 8 x 256）的特征图。在图片分类和目标检测的CNN网络中，特征图的长宽是逐渐减小的(本例中从128减小到8)，而通道数是增加的(本例中是从3增加到256)。此外，可以看到Pooling层是没有需要训练的参数的。那你可能会问了，我们将输入图变成8x8x256的特征图以后有什么用呢？这个我们以后再说。

FEATURED TAGS
deeplearning